Unveiling The Power Of Karnaugh Maps: A Comprehensive Guide To Simplifying Boolean Expressions With Three Variables

Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions with Three Variables

Related Articles: Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions with Three Variables

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions with Three Variables. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions with Three Variables

The realm of digital logic design often involves intricate Boolean expressions, which can be challenging to simplify and implement efficiently. Fortunately, a powerful tool known as the Karnaugh map (K-map) emerges as a visual aid, simplifying this process for expressions involving up to five variables. This article delves into the intricacies of K-maps for three variables, showcasing their application in minimizing Boolean expressions and ultimately streamlining digital circuit design.

Understanding the Fundamentals: A Visual Representation of Boolean Functions

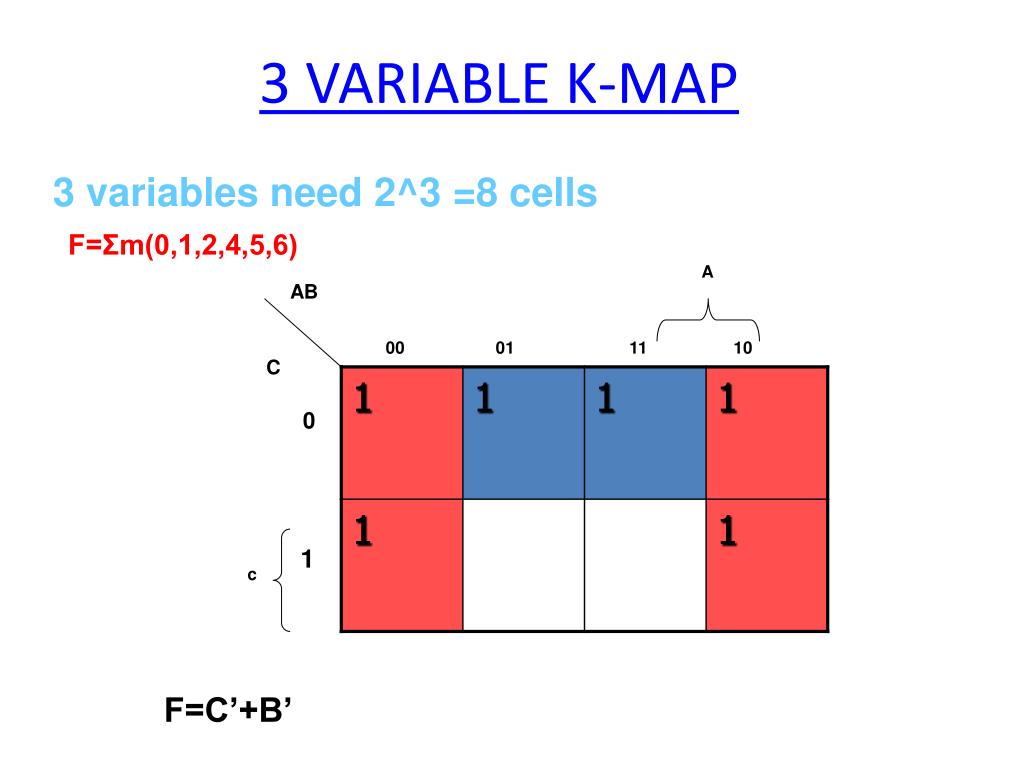
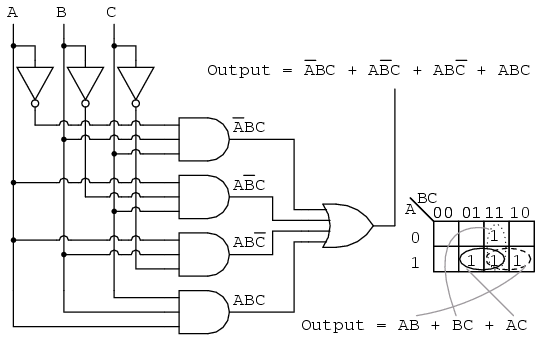
A Karnaugh map is a graphical representation of a Boolean function, providing a structured framework for simplifying complex expressions. For three variables, the K-map takes the form of a 2×4 grid, where each cell represents a unique combination of the input variables. The rows and columns are labeled with binary codes, ensuring that adjacent cells differ in only one variable.

Constructing a Karnaugh Map for Three Variables:

1. Define the Variables: Identify the three variables involved in the Boolean expression. Let’s assume these variables are A, B, and C.

2. Create the Grid: Construct a 2×4 grid with rows representing the combinations of variables A and B, and columns representing variable C.

3. Label the Rows and Columns: Assign binary values to the rows and columns, ensuring that adjacent cells differ in only one variable. For instance, the rows can be labeled 00, 01, 11, and 10, while the columns can be labeled 0 and 1.

4. Populate the Cells: Based on the truth table or Boolean expression, assign a ‘1’ or ‘0’ to each cell, corresponding to the output value for the specific input combination.

Example:

Consider the Boolean expression: F(A, B, C) = A’BC + AB’C’ + ABC’ + ABC.

The K-map for this expression would be populated as follows:

	C = 0	C = 1
AB = 00	0	0
AB = 01	0	1
AB = 11	1	1
AB = 10	1	0

The Essence of Simplification: Grouping Adjacent ‘1’s

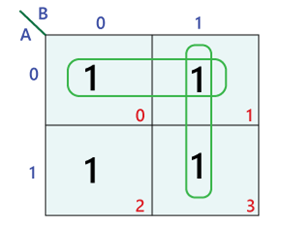
The true power of K-maps lies in their ability to simplify Boolean expressions by visually identifying and grouping adjacent ‘1’s. This process relies on the following key principles:

• Adjacent Cells: Cells are considered adjacent if they share a common edge and differ in only one variable. This includes cells that appear to be at the edge of the map but are actually adjacent due to the map’s wraparound nature (e.g., the top and bottom rows, or the leftmost and rightmost columns).

• Grouping ‘1’s: Adjacent ‘1’s are grouped together to form rectangular blocks, with the goal of maximizing the size of each block. The blocks can be of any size as long as they are rectangular and contain a power of two number of ‘1’s (e.g., 1, 2, 4, 8, etc.).

• Minimizing the Expression: Each block represents a simplified product term in the Boolean expression. The variable that changes within a block is eliminated from the product term, while the variables that remain constant are included.

Simplifying the Example:

In the example above, we can identify two groups of ‘1’s:

• Group 1: The ‘1’s in cells AB=11, AB=10, AB=01. This group represents the product term A’C.

• Group 2: The ‘1’s in cells AB=11, AB=10, AB=00. This group represents the product term BC’.

Therefore, the simplified Boolean expression is: F(A, B, C) = A’C + BC’.

Beyond Simplification: Unveiling the Importance of Karnaugh Maps

The ability to simplify Boolean expressions is just one of the many advantages offered by Karnaugh maps. Their significance extends to diverse aspects of digital logic design:

• Circuit Optimization: Simplified Boolean expressions translate into simpler and more efficient digital circuits, reducing the number of gates required and minimizing power consumption.

• Error Detection: Karnaugh maps can help identify potential errors in Boolean expressions by highlighting inconsistencies or redundancies in the grouping of ‘1’s.

• Design Verification: They provide a visual representation of the Boolean function, making it easier to understand and verify the logic behind the design.

• Design Exploration: K-maps facilitate exploring different design options by enabling the comparison of different groupings of ‘1’s and their resulting simplified expressions.

FAQs: Addressing Common Queries about Karnaugh Maps for Three Variables

1. Can a K-map be used for expressions with more than three variables?

Yes, K-maps can be used for up to five variables. However, the complexity of the map increases with the number of variables. For four variables, a 2x4x2 cube is used, and for five variables, a 2x4x2x2 hypercube is required.

2. What happens if a cell in the K-map has a ‘don’t care’ condition?

A ‘don’t care’ condition indicates that the output value for a specific input combination is irrelevant. These cells can be treated as either ‘1’ or ‘0’ during the grouping process, depending on which option leads to a simpler expression.

3. Is there a specific order for labeling the rows and columns in a K-map?

Yes, the rows and columns are labeled in a Gray code sequence, where adjacent values differ in only one bit. This ensures that adjacent cells differ in only one variable.

4. Can K-maps be used for functions with multiple outputs?

Yes, a separate K-map can be created for each output function.

5. What are the limitations of Karnaugh maps?

While powerful, K-maps become increasingly complex and challenging to use for expressions with more than five variables. For larger expressions, other simplification techniques like Quine-McCluskey minimization are employed.

Tips for Mastering Karnaugh Maps: A Guide to Efficient Application

• Practice: The key to mastering K-maps is through consistent practice. Solve numerous examples involving different Boolean expressions to gain familiarity with the grouping process and simplification techniques.

• Visualize the Map: Visualize the map mentally, particularly the wraparound nature of the edges. This will help you identify adjacent cells and form appropriate groupings.

• Start with Smaller Groups: Begin by identifying smaller groups of ‘1’s and gradually expand them to larger blocks.

• Don’t Overlook ‘Don’t Cares’: Utilize ‘don’t care’ conditions strategically to simplify the expression further.

• Verify Your Solution: After simplifying the expression, verify your result by comparing it to the original truth table or Boolean expression.

Conclusion: Embracing the Power of Visual Simplification

Karnaugh maps offer a powerful and intuitive approach to simplifying Boolean expressions, facilitating the design and optimization of digital circuits. By providing a visual representation of the Boolean function, K-maps enable the identification of patterns and the creation of simplified expressions, ultimately leading to more efficient and cost-effective designs. Mastering the art of K-map manipulation empowers engineers and designers to tackle complex logic problems with ease and confidence, paving the way for innovative and streamlined digital systems.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions with Three Variables. We hope you find this article informative and beneficial. See you in our next article!